Taller de
Razonamiento Cuantitativo
1) Si el valor de alquilado de un auto por día es de $100.000 y adicionalmente se paga $1.000 pesos por cada kilómetro recorrido. Si alquilamos el auto por dos días y la cuenta por pagar fue de $390.000. ¿Cuántos kilómetros recorrimos?
22) Una empresa de raíces chinas y champiñones vendieron en un día $400.000. Si se vendieron 30 bandejas de champiñón a $4.000. Si el precio de bandeja de raíz china es de $800 cada una. ¿Cuántas bandejas de raíz china se vendieron?
33) Un padre tiene el triple de la edad de su hijo. Si la suma de ambas edades es 56, ¿Qué edad tiene el hijo?
44) Dos números consecutivos suman 79. ¿Cuáles son?
55) Tres canastas contienen 245 manzanas. La primera canasta tiene 15 manzanas más que la segunda y 25 más que la tercera. ¿Cuántas manzanas hay en cada canasta?
Realizar el taller con el siguiente link
https://wordwall.net/play/35421/062/178
Quinta Guía y Taller de
Razonamiento Cuantitativo
Regla de tres simple
La regla de tres simple es una herramienta matemática que sirve para resolver rápidamente problemas que involucran una relación de proporcionalidad directa entre dos variables.
La regla de 3 simple es una operación que nos ayuda a resolver rápidamente problemas de proporcionalidad, tanto directa como inversa.
Para hacer una regla de tres simple necesitamos 3 datos: dos magnitudes proporcionales entre sí, y una tercera magnitud. A partir de estos, averiguaremos el cuarto término de la proporcionalidad.
En la vida diaria la regla de tres tiene diversas aplicaciones, tales como:
- Calcular costos, mediante la proporción lineal.
- Generar proporciones, por ejemplo de comida.
- Calcular el ingreso y los gastos en un día diario.
- Utilizarla para calcular el tiempo que se tardan en construir un edificio, o hacer renovaciones.
Regla de 3 simple directa
Empezaremos viendo cómo aplicarla en casos de proporcionalidad directa (cuando aumenta una magnitud también lo hace la otra).
Colocaremos en una tabla los 3 datos (a los que llamamos «a», «b» y «c») y la incógnita, es decir, el dato que queremos averiguar (que llamaremos “x”). Después, aplicaremos la siguiente fórmula:
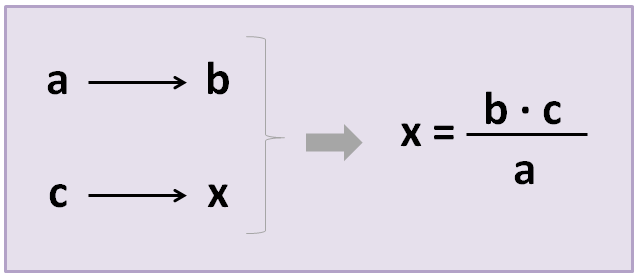
Para ver un ejemplo, vamos a resolver el mismo problema de proporcionalidad directa que vimos la semana pasada, ahora aplicando la regla de 3 simple.
1) Problema de regla de 3 simple directa
Al llegar al hotel nos han dado un mapa con los lugares de interés de la ciudad, y nos han dicho que 5 centímetros del mapa representan 600 metros de la realidad. Hoy queremos ir a un parque que se encuentra a 8 centímetros del hotel en el mapa. ¿A qué distancia del hotel se encuentra este parque?
Vamos a hacer la tabla con los 3 datos y la incógnita (“x”), y hallaremos “x” con la fórmula que acabamos de aprender:
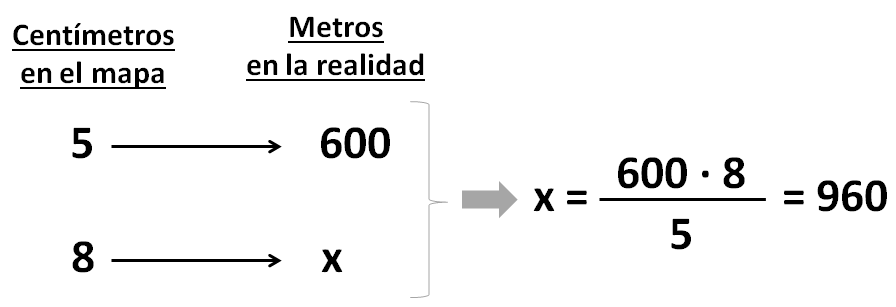
Solución: El parque se encuentra a 960 metros del hotel
2) Problema de regla de 3 simple directa
Un automóvil recorre 240 km en 3 horas. ¿Cuántos kilómetros habrá recorrido en 2 horas? Son magnitudes directamente proporcionales, ya que a menos horas recorrerá menos kilómetros.
240 km
3 h
x km 
2 h
Regla de 3 simple inversa
Ahora vamos a ver cómo aplicar la regla de 3 simple en casos de proporcionalidad inversa (cuando aumenta una magnitud disminuye la otra).
Colocaremos los 3 datos y la incógnita en la tabla igual que los hemos colocado en el caso anterior. Pero aplicaremos una fórmula distinta:
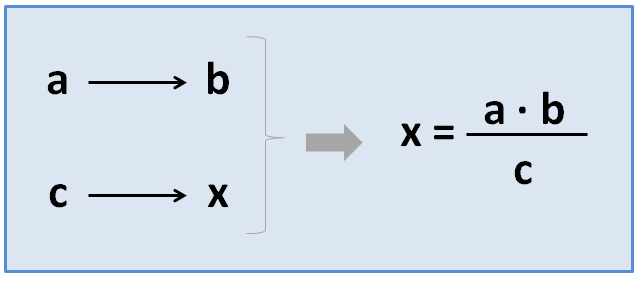
La regla de tres inversa la aplicaremos cuando entre las magnitudes se establecen las relaciones:
A más 
menos.
A menos 
más.
Problema de regla de 3 simple inversa
Vamos a ver un ejemplo
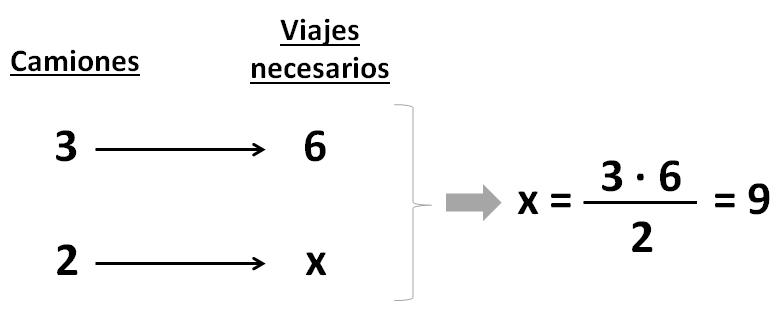
1) Ayer 2 camiones transportaron una mercancía desde el puerto hasta el almacén. Hoy 3 camiones, iguales a los de ayer, tendrán que hacer 6 viajes para transportar la misma cantidad de mercancía del almacén al centro comercial. ¿Cuántos viajes tuvieron que hacer ayer los camiones?
Colocamos los datos en una tabla y aplicamos la fórmula de la regla de 3 simple inversa:
2) Un grifo que mana 18 l de agua por minuto tarda 14 horas en llenar un depósito. ¿Cuánto tardaría si su caudal fuera de 7 l por minuto?
Son magnitudes inversamente proporcionales, ya que a menos litros por minuto tardará más en llenar el depósito.
18 l/min 
14 h
7 l/min 
x h
Taller
1) Un automóvil recorre 180 km en 3 horas.
¿Cuántos kilómetros habrá recorrido en 2 horas?
¿Cuánto tiempo dudará en recorrer 270 kilómetros?
Son magnitudes directamente proporcionales, ya que a menos horas recorrerá menos kilómetros.
2) 3 obreros construyen un muro en 12 horas, ¿Cuánto tardarán en construirlo 6 obreros?
Son magnitudes inversamente proporcionales, ya que a más obreros tardarán menos horas.
3) 20 policías consumen 140 kilos de comida, calcular ¿Cuánta comida consumen 56 policías?
Regla de tres compuesta directa
La regla de tres compuesta se emplea cuando se relacionan tres o más magnitudes, de modo que a partir de las relaciones establecidas entre las magnitudes conocidas obtenemos la desconocida.
Una regla de 3 compuesta se compone de varias reglas de 3 simples aplicadas sucesivamente.
Como entre las magnitudes se pueden establecer relaciones de proporcionalidad directa o inversa, podemos distinguir tres casos de regla de tres compuesta
Nueve grifos abiertos durante 10 horas diarias han consumido una cantidad de agua por valor de 20 €. Averiguar el precio del vertido de 15 grifos abiertos 12 horas durante los mismos días.
A más grifos, más euros 
Directa.
A más horas, más euros 
Directa.
9 grifos 
10 horas 
20 €
15 grifos 
12 horas 
x €
Regla de tres compuesta inversa
5 obreros trabajando, trabajando 6 horas diarias construyen un muro en 2 días. ¿Cuánto tardarán 4 obreros trabajando 7 horas diarias?
A menos obreros, más días
Inversa.
A más horas, menos días
Inversa.
5 obreros 
6 horas 
2 días
4 obreros 
7 horas 
x días
TALLER
Resolver los ejercicio de cualquier metodo
1)
2)
3)
4)
![100\xrightarrow[\; \; \; \; \; ]{}7](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-f238d22e1f029e83e5c22e54cca18e42_l3.png "Rendered by QuickLaTeX.com")
![\begin{matrix} \textup{Cantidad inicial} & \xrightarrow[\; \; \; \; \; ]{} &\textup{Cantidad relacionada con el porcentaje} \\ & & \\ 100 & \xrightarrow[\; \; \; \; \; ]{} & \textup{Porcentaje}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \end{matrix}](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-80167647b07755d65a19d260b9d106b9_l3.png "Rendered by QuickLaTeX.com")
