Segunda  Guía y  Taller  de

 Razonamiento Cuantitativo

OPERACIONES CON FRACCIONES

Como las fracciones son números, es lógico que se puedan sumar y restar. Estas operaciones son fáciles de calcular, aunque se realizan de forma distinta según si los denominadores de las fracciones son iguales o distintos.

Recordad que el numerador es el número sobre la raya de la fracción y el denominador es el que esta debajo de la raya. Por ejemplo,

Fracciones homogéneas

Suma de fracciones homogéneas

La suma de dos fracciones con el mismo denominador se calcula sumando sus numeradores. El denominador se mantiene.

 

EJEMPLO  1

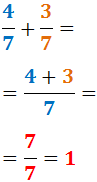
Representación gráfica:

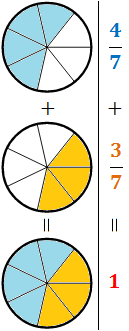
EJEMPLO  2

Resta de fracciones homogéneas

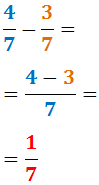
Fracciones heterogéneas

Suma de fracciones heterogéneas

Se puede hacer por dos métodos, el método del mínimo común denominador para la suma o resta de dos o más fracciones y el método de la multiplicación en cruz para la suma o resta de dos fracciones. El método más utilizado el el del mínimo común denominador.

Segunda forma:

La suma de dos o más fracciones heterogéneas se realiza de la siguiente manera:

1. Se halla el mínimo común múltiplo de los dos denominadores.
2. Se calculan los numeradores con la fórmula: numerador por denominador común y dividido por denominador.
3. Se suman los numeradores (dado que las fracciones modificadas tienen el mismo denominador).

Suma de fracciones de distinto denominador

Ejemplo:

1. Se calcula el mínimo común múltiplo (m.c.m.), por lo que se tiene que 

2. Se calculan los numeradores.

• Numerador de la primera fracción: 
• Numerador de la segunda fracción: 
• La suma se reduce a las siguientes fracciones:
  

3. Se suman los numeradores:

.

ejemplo 2

1/6 + 4/9 = 3/18 + 8/18 = 11/18

Taller

 

Taller 

1)      9/4 +5/4=

2)   7/3 + 2/3 + 5/3 + 8/3 =

3)  2/3+1/4 =

4)  3/4 -1/2 =

5)  2/3 - 5/6

6)  1/2 + 4/3 + 5/9 =

Ejercicios con fraccionarios

1)En un parqueadero hay 22 autos,  7  son de marca Daewoo

 ¿conque fracción representamos los autos Daewoo en el

    parqueadero? 

2)   Josefa  se ha gastado  1/3 del dinero que le dieron sus

 abuelos comprando un libro. También se compro 1/9

  comprando un vestido. ¿Qué fracción se ha gastado Josefa?

3) Felipe compró 1 kilo de Camarones. En el almuerzo se gastó  3/4 del kilo. ¿Qué cantidad de camarones le quedaron para otro almuerzo?

4) Resolver:    7/8+3/10  de las dos formas

5) Resolver     -5/4-2/3    de las dos formas