Primera Guía y Taller de
Razonamiento Cuantitativo
Razonamiento cuantitativo
El razonamiento cuantitativo es el conjunto de elementos de las matemáticas, sean estos conocimientos o competencias, que permiten a un ciudadano tomar parte activa e informada en los contextos social, cultural, político, administrativo, económico, educativo y laboral.
La competencia la entiende como un conjunto de conocimientos, habilidades, actitudes, comprensiones y disposiciones cognitivas, socioafectivas y psicomotoras apropiadamente relacionadas entre sí para facilitar el desempeño flexible, eficaz y con sentido de una actividad o de cierto tipo de tareas en contextos relativamente nuevos y retadores.
El razonamiento cuantitativo se refiere al conjunto de habilidades que despliega una persona para comprender, analizar, argumentar, tomar decisiones y generar estrategias para la solución de situaciones que contengan información que pueda ser tratada de manera cuantitativa.
Ejemplo:
1) https://www.youtube.com/watch?v=4uLDjlFMm40
ejemplo con fraccionarios
2) https://www.youtube.com/watch?v=rBCBXnFwvjA
Números reales ℜ.
Los números reales son el conjunto que incluye los números naturales (1,2,3,4,5,6,7...) , enteros, racionales e irracionales. Se representa con la letra ℜ.
Números naturales
Los números naturales son un conjunto de números discreto que pertenece a la recta real y puede o no incluir el número cero (0).
En otras palabras, los números naturales son el primer conjunto de números que aprendemos cuando somos pequeños y utilizamos para contar. los números naturales son los números que usamos “naturalmente” para contar.
Expresión
Los números naturales se expresan con la letra: N
Números Racionales
Los números racionales, son el conjunto de números fraccionarios y números enteros representados por medio de fracciones. Al conjunto de los números racionales se lo denota con la letra ℚ, que viene de la palabra anglosajona “Quotient” traducción literal de cociente, y que sirve para recogerlos como subgrupo dentro de los números reales y junto a los números enteros
Y ¿qué son los números racionales? Son todos los números que se pueden representar por una fracción. Si no se puede representar con una fracción, lo llamamos número irracional.
Números irracionales
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es ![]() , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
![]()
Por ejemplo:
Expresar 0,75 como fracción
Paso 1: Escribe:
0,75 |
1 |
Paso 2: Multiplica el numero de abajo y el de arriba por 100 (porque hay 2 dígitos luego de la coma):
× 100 | ||
0,75 | = | 75 |
1 | 100 | |
× 100 | ||
(¿Ves como el número de arriba se convierte
en un entero?)
Paso 3: Simplifica la fracción:
÷ 25 | ||
75 | = | 3 |
100 | 4 | |
÷ 25 | ||
Respuesta = ¾
Ejemplo 2: Expresa 0,625 como una fracción
Paso 1: escribe
0,625 |
1 |
625 |
1.000 |
| ÷ 25 | | ÷ 5 | |
| ||||
625 | = | 25 | = | 5 |
1,000 | 40 | 8 | ||
| ||||
| ÷ 25 | | ÷ 5 | |
Respuesta = 5/8
Taller
1) Expresa 0,333 como fracción
2) Expresa 0,97 como fracción
3) Expresa 0,125 como fracción
4) Expresa 4 como fracción
5) Expresa 5 como fracción
1)
2) 3/5
3) 1/3
Segunda Guía y Taller de
Razonamiento Cuantitativo
OPERACIONES CON FRACCIONES
Como las fracciones son números, es lógico que se puedan sumar y restar. Estas operaciones son fáciles de calcular, aunque se realizan de forma distinta según si los denominadores de las fracciones son iguales o distintos.
Recordad que el numerador es el número sobre la raya de la fracción y el denominador es el que esta debajo de la raya. Por ejemplo,
Fracciones homogéneas
Suma de fracciones homogéneas
La suma de dos fracciones con el mismo denominador se calcula sumando sus numeradores. El denominador se mantiene.
EJEMPLO 1
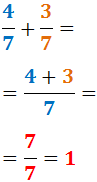
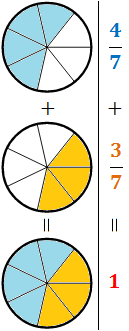
Representación gráfica:
EJEMPLO 2

Resta de fracciones homogéneas
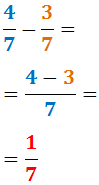
Fracciones heterogéneas
Suma de fracciones heterogéneas
Segunda forma:
La suma de dos o más fracciones heterogéneas se realiza de la siguiente manera:
- Se halla el mínimo común múltiplo de los dos denominadores.
- Se calculan los numeradores con la fórmula: numerador por denominador común y dividido por denominador.
- Se suman los numeradores (dado que las fracciones modificadas tienen el mismo denominador).
Ejemplo:
1. Se calcula el mínimo común múltiplo (m.c.m.), por lo que se tiene que
2. Se calculan los numeradores.
- Numerador de la primera fracción:
- Numerador de la segunda fracción:
- La suma se reduce a las siguientes fracciones:
3. Se suman los numeradores:
- .
- ejemplo 2
- 1/6 + 4/9 = 3/18 + 8/18 = 11/18
- Taller
Taller
1) 9/4 +5/4=
2) 7/3 + 2/3 + 5/3 + 8/3 =
3) 2/3+1/4 =
4) 3/4 -1/2 =
5) 2/3 - 5/6
6) 1/2 + 4/3 + 5/9 =





















No hay comentarios:
Publicar un comentario