Segunda  Guía y  Taller  de

 Razonamiento Cuantitativo

OPERACIONES CON FRACCIONES

Como las fracciones son números, es lógico que se puedan sumar y restar. Estas operaciones son fáciles de calcular, aunque se realizan de forma distinta según si los denominadores de las fracciones son iguales o distintos.

Recordad que el numerador es el número sobre la raya de la fracción y el denominador es el que esta debajo de la raya. Por ejemplo,

Fracciones homogéneas

Suma de fracciones homogéneas

La suma de dos fracciones con el mismo denominador se calcula sumando sus numeradores. El denominador se mantiene.

 

EJEMPLO  1

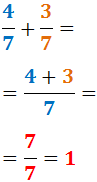
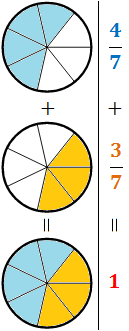
Representación gráfica:

EJEMPLO  2

Resta de fracciones homogéneas

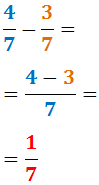
Fracciones heterogéneas

Suma de fracciones heterogéneas

Se puede hacer por dos métodos, el método del mínimo común denominador para la suma o resta de dos o más fracciones y el método de la multiplicación en cruz para la suma o resta de dos fracciones. El método más utilizado el el del mínimo común denominador.

Cuando dos o más fracciones tienen denominadores distintos se dicen heterogéneas. No es posible sumar este tipo de fracciones como se hizo con las homogéneas, debido a que representan distintos tipos de objetos.  Observa el siguiente ejemplo, realicemos la suma .

Si representamos las unidades con círculos entonces las expresiones  y  se pueden representar así:

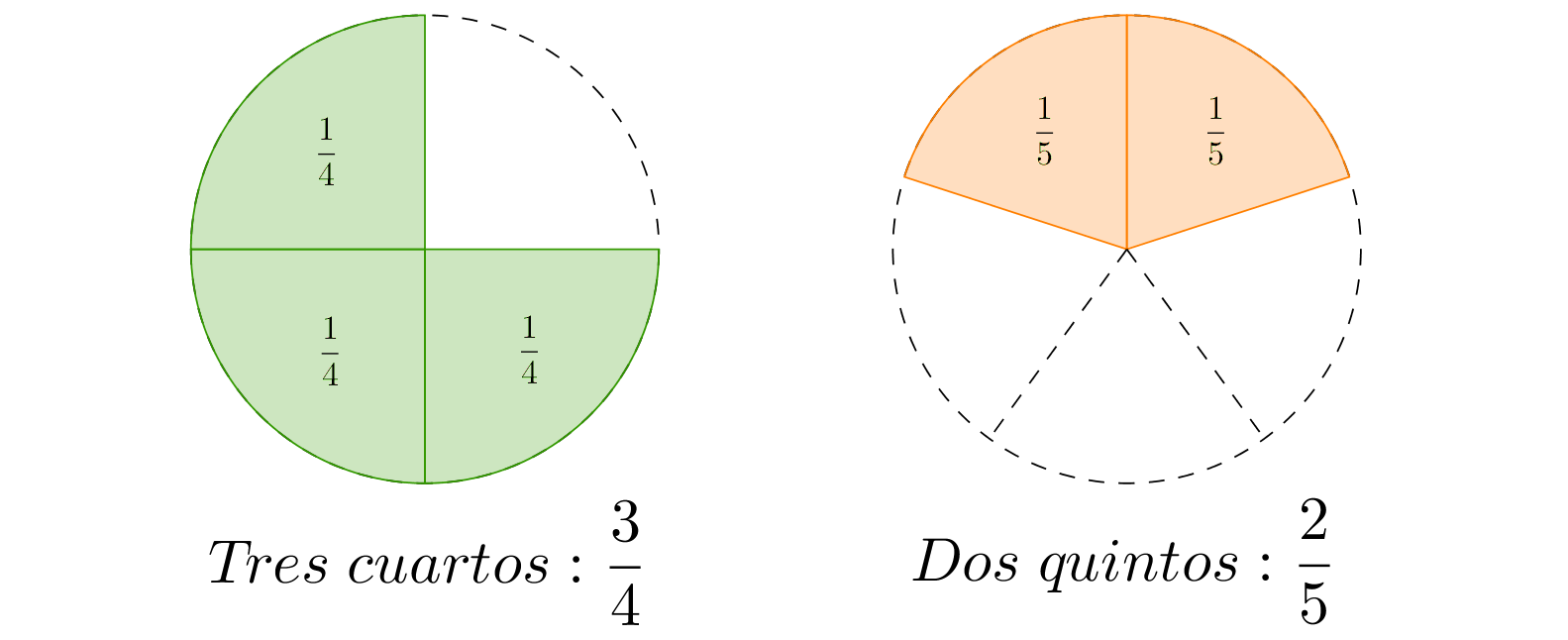
Para entender por qué no es correcto sumar los numeradores como en el caso de las fracciones homogéneas, piensa en lo siguiente: ¿cuánto son tres manzanas más dos naranjas?  Si piensas que la respuesta es cinco deberías preguntarte cinco qué: ¿cinco manzanas, o cinco naranjas?  

Claramente no son ni cinco manzanas ni cinco naranjas, así que dicha respuesta carece de sentido.  Así, si se sumaran los numeradores de las fracciones, se tendría el mismo inconveniente que con las manzanas y las naranjas: , porque no serían ni cinco cuartos ni cinco quintos.

Cuando sumes fracciones heterogéneas puedes seguir los siguientes pasos.

Para resumir el anterior procedimiento se usa la fórmula:

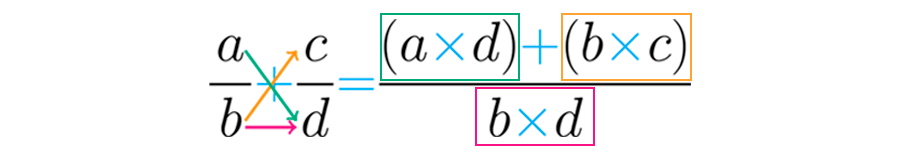
Siempre que sea posible se debe simplificar el resultado de la suma, por ejemplo:

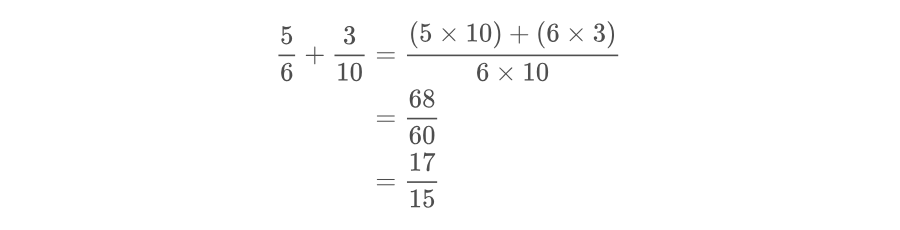
En este caso el resultado de la suma es sesenta y ocho sesentavos, sin embargo después de simplificar se puede decir que es diecisiete quinceavos.

Segunda forma:

La suma de dos o más fracciones heterogéneas se realiza de la siguiente manera:

1. Se halla el mínimo común múltiplo de los dos denominadores.
2. Se calculan los numeradores con la fórmula: numerador por denominador común y dividido por denominador.
3. Se suman los numeradores (dado que las fracciones modificadas tienen el mismo denominador).

Suma de fracciones de distinto denominador

Ejemplo:

1. Se calcula el mínimo común múltiplo (m.c.m.), por lo que se tiene que 

2. Se calculan los numeradores.

• Numerador de la primera fracción: 
• Numerador de la segunda fracción: 
• La suma se reduce a las siguientes fracciones:
  

3. Se suman los numeradores:

.

ejemplo 2

1/6 + 4/9 = 3/18 + 8/18 = 11/18

Taller

 

                                                         Problema 2     

                                          Un pedazo de alambre mide 5/6 de metro. De este

                                          pedazo se utiliza  1/2 de metro. ¿Cuánto mide 

                                          el pedazo que sobra?                          

Taller 

1)      9/4 +5/4=

2)   7/3 + 2/3 + 5/3 + 8/3 =

3)  2/3+1/4 =

4)  3/4 -1/2 =

5)  2/3 - 5/6

6)  1/2 + 4/3 + 5/9 =

viernes, 28 de abril de 2023

Tercera   Guía y  Taller  de

 Razonamiento Cuantitativo

Ecuaciones

 

Una ecuación en matemática se define como una igualdad establecida entre dos expresiones, en la cual puede haber una o más incógnitas que deben ser resueltas.

Las ecuaciones sirven para resolver diferentes problemas matemáticos, geométricos, químicos, físicos o de cualquier otra índole, que tienen aplicaciones tanto en la vida cotidiana como en la investigación y desarrollo de proyectos científicos.

Las ecuaciones pueden tener una o más incógnitas, y también puede darse el caso de que no tengan ninguna solución o de que sea posible más de una solución.

Partes de una ecuación

Las ecuaciones están formadas por diferentes elementos. Veamos cada uno de ellos.

Cada ecuación tiene dos miembros, y estos se separan mediante el uso del signo igual (=).

Cada miembro está conformado por términos, que corresponden a cada uno de los monomios.

Los valores de cada monomio de la ecuación pueden ser de diferente tenor. Por ejemplo:

·         constantes;

·         coeficientes;

·         variables;

·         funciones;

·         vectores.

Las incógnitas, es decir, los valores que se desean encontrar, se representan con letras. Veamos un ejemplo de ecuación.

Ejercicios de ecuaciones primer grado

1)   2x - 34 = 120

1. Se hace la transposición de términos.

2x = 120 + 34

2. Se reducen los términos semejantes.

2x = 154

3. Se despeja la incógnita.

x =154/2 = 77

2)   10x + 5 = 3x + 12

1. Se hace la transposición de términos.

10x - 3x = 12 - 5

2. Se reducen los términos semejantes.

7x = 7

3. Se despeja la incógnita.

x = 7/7 = 1

3)   2(3x - 2) = 8

1. Se suprimen los paréntesis.

6x - 4 = 8

2. Se hace la transposición de términos.

6x = 8 + 4

3. Se reducen los términos semejantes.

6x = 12

3. Se despeja la incógnita.

x = 12/6 = 2

4)   (x + 2)² - x² = 60

1. Se suprimen los paréntesis desarrollando la potencia.

x² + 4x + 4 - x² = 60

2. Se hace la transposición de términos.

x² - x² + 4x = 60 - 4

3. Se reducen los términos semejantes.

4x = 56

4. Se despeja la incógnita.

x = 56/4 = 14

                                  Taller

1) 5x+4=1-x

2) 3.(x-5)=6

3) 4(2x+1)=x+4

4) 3-x=3.(x+5)

5) 2(3x - 6 + 5x - 15) + x = - 8

6) (x + 2)² - x² = 60